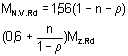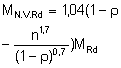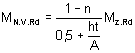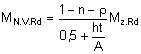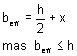Artigo 35.º

Esforço transverso

 

1. O valor de cálculo do esforço transverso V_Sd em cada secção transversal deve satisfazer:

 

 

V_Sd  £  V_pl.Rd

 

em que V_pl.Rd é o valor de cálculo da resistência plástica ao esforço transverso dado por

 

V_pl.Rd = A_v  / g_M0

 

2. A área de corte A_v pode ser calculada utilizando o Quadro 16.

 

3. Nos outros casos, o valor de A_v deve ser determinado de forma análoga.

 

4. Não é necessário ter em conta os furos para ligações nas verificações ao esforço transverso desde que:

 

A_v.net  ³ (f_y / f_u) A_v

 

Quando A_v.net for inferior a este limite, pode admitir-se uma área efectiva de corte com o valor de (f_y / f_u) A_v.net.

 

5. A resistência à encurvadura por esforço transverso deve também ser verificada, tal como especificado no artigo 40.º quando:

 

  no caso de uma alma não reforçada

 

  no caso de uma alma reforçada

 

em que  k_t = coeficiente de encurvadura (ver Quadro 21)

 

               

 

6. O critério de rotura por esforço transverso apresentado no artigo 50.º deverá também ser verificado nas extremidades de um elemento.

 

Artigo 36.º

Flexão, esforço transverso e forças axiais

 

1. Para as secções transversais das Classes 1 e 2, os seguintes critérios devem ser satisfeitos:

 

1) Força axial:  (ver artigos 32.º ou 33.º)

 

2) Esforço transverso:  (ver artigo 35.º)

 

3) Momento flector:  (ver Quadro 17)

em que M_N.V.Rd é o valor de cálculo reduzido do momento plástico tendo em conta a força axial e o esforço transverso.

 

4) Momento flector biaxial (flexão desviada):

 

 

2. Para as secções transversais da Classe 3, os seguintes critérios devem ser satisfeitos:

 

1) Força axial:  (ver artigos 32.º ou 33.º)

 

2) Esforço transverso:  (ver artigo 35.º)

 

3) Momento flector:  (ver artigo 34.º)

 

4) Fórmula de interacção:

 

 para

 

 para

 

em que:r = (2 V_Sd / V_pl.Rd – 1)²

 

3. A resistência à encurvadura do elemento e à encurvadura lateral deve também ser verificada. (ver Secção III)

 

 

 

SECÇÃO III

Resistência à encurvadura dos elementos

 

Artigo 37.º

Resistência à encurvadura de elementos comprimidos

 

1. O valor de cálculo da resistência à encurvadura de um elemento comprimido deve verificar:

 

N_Sd  £  N_b.Rd

 

em que N_b.Rd é dado por N_b.Rd = cb_A A f_y / g_M1

 

b_A     = 1 para secções transversais de Classes 1, 2 ou 3

 

b_A    = A_eff / A para secções transversais de Classe 4

 

c       = factor de redução para o modo de encurvadura relevante

 

2. Para secções transversais uniformes, o valor de c pode ser determinado a partir da seguinte expressão:

 

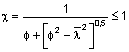
em que:     

 

                   a = factor de imperfeição (ver Quadro 18)

 

3. A esbelteza adimensional  é dada por:

 

 

em que:         

 

       com                 (f_y – N/mm²)

 

                         _{= esbelteza}

 

4. A esbelteza  pode ser calculada através da seguinte expressão:

 

 

em que  =    comprimento de encurvadura de um elemento comprimido, com as duas extremidades impedidas de se deslocarem lateralmente, pode, conservativamente, ser considerado igual ao seu comprimento nominal L.

 

i =     raio de giração da secção transversal bruta, em relação ao eixo apropriado.

 

5. Para elementos de secção transversal variável ao longo do seu comprimento, os valores de c podem ser verificados através de uma análise de segunda ordem.

 

 

 

Artigo 38.º

Resistência à encurvadura de elementos em flexão composta com compressão

 

1. Os elementos com secções transversais das Classes 1 e 2 sujeitas a uma combinação de flexão e compressão devem satisfazer a condição:

 

 

em que:

 

 

 

 

    =  menor dos valores de  e .

 

,,,    =  obtidos a partir do artigo 37.º

 

,        =    factores de momento uniforme equivalente, correspondentes à encurvadura por varejamento (ver Quadro 19 e parágrafo 4)

 

2. Os elementos com secções transversais das Classes 1 e 2 para os quais a encurvadura lateral é um modo de colapso possível devem satisfazer igualmente a condição:

 

 

em que:

 

 

 

, = obtidos a partir do artigo 39.º

 

  factor de momento uniforme equivalente, correspondente à encurvadura lateral (ver Quadro 19 e parágrafo 4)

 

3. A verificação de resistência à encurvadura para os elementos das Classes 3 e 4 deve seguir o descrito no capítulo 5.5.4 de ENV1993-1-1.

 

4. Os factores de momento uniforme equivalente b_M.y,b_M.z,b_M.LT devem ser obtidos a partir do Quadro 19, de acordo com a forma do diagrama de momentos de flexão, entre pontos contraventados do seguinte modo:

 

 

 

 

Artigo 39.º

Encurvadura lateral de vigas

 

1. Não é necessário verificar a resistência à encurvadura lateral de vigas com contraventamento lateral.

 

2. O valor de cálculo do momento resistente à encurvadura lateral de uma viga sem contraventamento lateral deve verificar:

 

M_Sd  £  M_b.Rd

 

Em que M_b.Rd é dado por

 

 

= 1 para secções transversais de Classe 1 ou Classe 2;

 

para secções transversais de Classe 3;

 

para secções transversais de Classe 4;

 

= factor de redução para a encurvadura lateral.

 

 

3. O valor de c_LT pode ser determinado a partir da expressão:

 

em que:

;

 

 para secções laminadas (curva a);

 

 para secções soldadas (curva c);

 

4. A esbelteza normalizada  pode ser determinada a partir da expressão:

 

 

em que:

 

;

 

    (f_y : N/mm²);          (ver artigo 37.º)

 

 

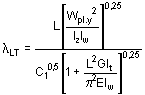
I_t = constante de torsão;

 

I_w = constante de enfunamento («warping»);

 

C₁ =     factor dependente da situação de carga e das condições de restrição de movimento, indicado por y e por k (ver Quadro 20);

 

y   =    relação do momento final entre as restrições de movimento lateral;

 

k   =     Factor de comprimento efectivo para rotação no plano, que é igual a 0,5 para uma fixação total e 1,0 sem qualquer fixação, sendo 0,7 para o caso em que uma extremidade está livre e a outra fixa.

 

5.    No caso em que a esbelteza normalizada , não é necessário considerar a encurvadura lateral.

 

 

 Artigo 40.º

Resistência à Encurvadura por Esforço Transverso

 

1. Bases

 

1)As almas com d/t_w superior a 69e para uma alma não reforçada, ou  (ver Quadro 21 para valores de k_t) para uma alma reforçada, devem ser verificadas quanto à resistência à  encurvadura por esforço transverso;

 

2) Para as almas sem reforços transversais intermédios e para as almas apenas com reforços transversais, a resistência à encurvadura por esforço transverso pode ser verificada utilizando:

 

Ÿ            O método simples de resistência pós-encurvadura – apresentado seguidamente;

Ÿ            O método do campo diagonal de tracções – consultar a cláusula 5.6 da ENV1993-1-1.

 

2. Método simples de resistência pós-encurvadura

 

1) No método simples de resistência pós-encurvadura, o cálculo do esforço transverso resistente à encurvadura V_ba.Rd deve verificar:

 

V_Sd  £  V_ba.Rd

 

em que V_ba.Rd é dado por

 

 é a resistência pós-encurvadura ao corte que depende da esbelteza da alma l_w (verQuadro 22);

 

2) A esbelteza da alma l_w é determinada a partir de:

 

 

em que k_t= coeficiente de encurvadura (ver Quadro 21).

 

            

  

 

3.    Momento flector e esforço transverso

 

1) Desde que V_Sd não exceda 50% de V_ba.Rd, a resistência de cálculo da secção transversal ao momento flector não tem que ser reduzida para ter em conta o esforço transverso;

 

2) Quando V_Sd excede 50 % de V_ba.Rd, a resistência de cálculo da secção transversal deve ser reduzida a M_v.Rd do seguinte modo:

 

 

em que: 

 

M_f.Rd = valor de cálculo da resistência à flexão plástica de uma secção transversal constituída apenas por banzos, tendo em conta a largura efectiva b_eff do banzo comprimido.

 

Artigo 41.º

Encurvadura do banzo no plano da alma

 

Para impedir a possibilidade do banzo comprimido encurvar no plano da alma, a relação d/t_w da alma deve satisfazer o critério seguinte:

 

 

em que:

 

A_w é a área da secção da alma;

 

A_fc é a área da secção do banzo comprimido;

 

f_yf  é a tensão de cedência do banzo comprimido;

 

k =    0,3 para banzos de Classe 1;

         0,4 para banzos de Classe 2;

         0,55 para banzos de Classe 3 ou Classe 4.

 

Artigo 42.º

Resistência da alma a forças transversais

 

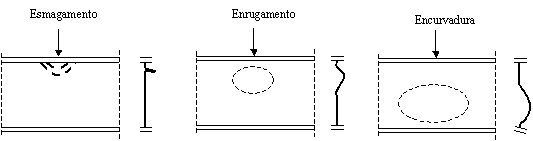
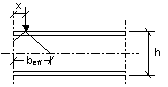
1. A resistência de uma alma não reforçada a forças transversais aplicadas através de um banzo é condicionada por um dos seguintes modos de colapso (ver Figura 2):

 

1) Esmagamento da alma junto ao banzo, acompanhado de deformação plástica do banzo;

 

2) Enrugamento da alma sob a forma de encurvadura e esmagamento localizado da alma junto ao banzo, acompanhados de deformação plástica do banzo;

 

3) Encurvadura da alma abrangendo a maior parte da altura da peça. 

 

 

2. Quando as forças são aplicadas através de um banzo e equilibradas por esforço transverso na alma, a resistência da alma às forças transversais deve ser considerada como o menor dos valores:

 

Ÿ           da resistência ao esmagamento R_y.Rd (ver parágrafo 4);

Ÿ           da resistência ao enrugamento R_a.Rd (ver parágrafo 5).

 

3. Nos casos em que as forças são aplicadas a um banzo e transferidas através da alma directamente ao outro banzo, a resistência da alma às forças transversais deve ser considerada como o menor dos valores:

 

Ÿ           da resistência ao esmagamento R_y.Rd (ver parágrafo 4);

Ÿ           da resistência à encurvadura R_b.Rd (ver parágrafo 6).

 

4. Resistência ao esmagamento R_y.Rd

 

O valor de cálculo da resistência ao esmagamento R_y.Rd da alma de uma secção I, H ou U deve ser obtido a partir de:

 

R_y.Rd = (s_s + s_y) t_w f_yw / g_M1

 

em que:

 

s_s = comprimento de apoio rígido;

 

 

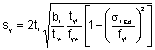
mas b_f não deve ser considerado superior a 25t_f e na extremidade de uma peça s_y deve ser reduzido a metade;

s_f.Ed é a tensão longitudinal do banzo.

 

5. Resistência ao enrugamento R_a.Rd

 

O valor de cálculo da resistência ao enrugamento R_a.Rd da alma de uma secção I, H ou U obtém-se a partir de:

 

 

Mas s_s/d não deve ser considerado superior a 0,2. Nos casos em que a peça também esteja sujeita a momentos flectores, devem ser satisfeitos os seguintes critérios:

 

 

 

 

6.    Resistência à encurvadura R_b.Rd

 

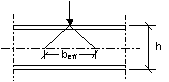
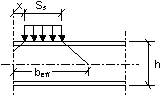
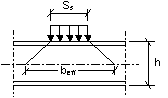
O valor de cálculo da resistência à encurvadura R_b.Rd da alma de uma Secção I, H ou U obtém-se considerando a alma como um elemento fictício comprimido com uma largura efectiva b_eff obtida a partir de:

 

    (ver Quadro 23)

 

A resistência à encurvadura deve ser determinada com base no artigo 37.º considerando a curva de encurvadura c e b_A=1.